🎯 Quick Answer
The Fibonacci sequence is a series of numbers where each number is the sum of the two numbers before it. It's like a mathematical recipe: take any two numbers, add them together, and you get the next number!
The sequence looks like this:
Starting numbers → Each new number = sum of previous two
🔢 What Makes It So Simple?
Imagine you're climbing stairs, but with a special rule: you can only take 1 or 2 steps at a time. The Fibonacci sequence works similarly - each new number is made by adding the two numbers that came before it.
🎯 Let's See How It Works!
📐 The Mathematical Rule
Translation: Any Fibonacci number = the previous number + the number before that
Starting values: F(0) = 0, F(1) = 1
📊 Building the Sequence Step by Step
Let's build the first 15 Fibonacci numbers together! Watch how each new number comes from adding the two before it:
🔢 The Fibonacci Sequence in Action
| Position | Fibonacci Number | How We Got It |
|---|---|---|
| F(0) | 0 | 🎯 Starting value |
| F(1) | 1 | 🎯 Starting value |
| F(2) | 1 | ➕ 0 + 1 = 1 |
| F(3) | 2 | ➕ 1 + 1 = 2 |
| F(4) | 3 | ➕ 1 + 2 = 3 |
| F(5) | 5 | ➕ 2 + 3 = 5 |
| F(6) | 8 | ➕ 3 + 5 = 8 |
| F(7) | 13 | ➕ 5 + 8 = 13 |
| F(8) | 21 | ➕ 8 + 13 = 21 |
| F(9) | 34 | ➕ 13 + 21 = 34 |
🤔 Try It Yourself!
Can you figure out the next three numbers in the sequence? Here's what we have so far:
Click to see the answer! 👆
The next three numbers are: 55, 89, 144
• 21 + 34 = 55
• 34 + 55 = 89
• 55 + 89 = 144
📚 The Fascinating History
🇮🇹 Meet Leonardo Fibonacci
Real name: Leonardo Pisano Bogollo
Lived: 1170-1250 (Italy)
Nickname: “Fibonacci” means “Son of Bonacci”
Famous for: Bringing Hindu-Arabic numerals (0,1,2,3...) to Europe!
📖 The Book That Started It All
Book: “Liber Abaci” (1202)
Meaning: “The Book of Calculation”
Purpose: Teaching European merchants how to use the new number system
Bonus: Included the famous rabbit problem!
🐰 The Famous Rabbit Problem
The Question Fibonacci Asked:
“If you start with one pair of rabbits, and every month each mature pair produces a new pair, and rabbits become mature after two months, how many pairs will you have after one year?”
The pattern: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
After 12 months: 144 pairs of rabbits! 🎉
🇮🇳 Plot Twist: India Knew It First!
While we call it the “Fibonacci sequence,” Indian mathematicians actually discovered it hundreds of years earlier! Scholars like Pingala (around 200 BC) used it to study Sanskrit poetry patterns. Fibonacci just introduced it to Europe!
✨ Amazing Properties & Patterns
🔲 Fibonacci Squares
When we arrange squares with Fibonacci side lengths, something beautiful happens - they fit together perfectly!
Each square's side length is a Fibonacci number: 1, 1, 2, 3, 5, 8, 13, 21...
🌀 The Famous Fibonacci Spiral
When we draw quarter-circles in each Fibonacci square, we get the beautiful Fibonacci spiral!
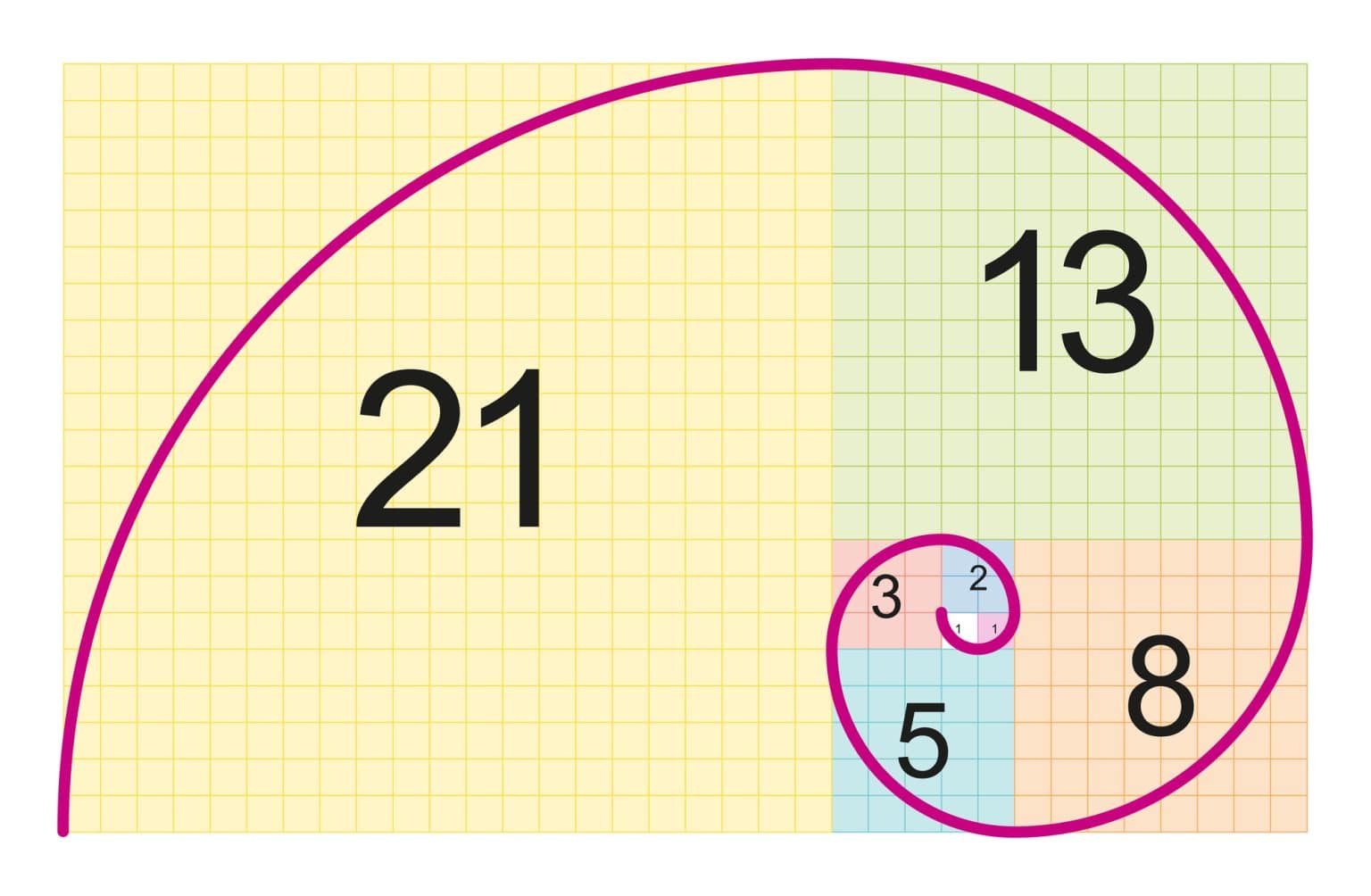
The red spiral approximates the Golden Spiral - found everywhere in nature!
🏆 The Golden Ratio Connection
Here's something magical: when you divide any Fibonacci number by the one before it, you get closer and closer to the Golden Ratio (φ ≈ 1.618)!
Watch the Magic Happen:
📐 Golden Rectangle
When you remove a square from a golden rectangle, you get another golden rectangle!
🌻 Fibonacci in Nature
Nature loves Fibonacci numbers! Here are some amazing examples you can see in real life:
🌻 Sunflower Seed Pattern

Fibonacci sequence in nature: 21 clockwise, 34 counterclockwise spirals
Lily
Buttercup
Delphinium
Marigold
Sunflowers
Seeds spiral in patterns of 21, 34, 55, or 89
Pinecones
Spirals often follow 8 and 13 pattern
Flower Petals
Many flowers have 3, 5, 8, 13, or 21 petals
Nautilus Shells
Chambers grow in Fibonacci proportions
Pineapples
Hexagonal patterns in 8 and 13 spirals
Tree Branches
Branching patterns follow Fibonacci ratios
🎯 Cool Number Patterns
🔢 Even-Odd Pattern
Pattern: Even, Odd, Odd, Even, Odd, Odd...
🔍 Divisibility Magic
• Every 3rd number is divisible by 2
• Every 4th number is divisible by 3
• Every 5th number is divisible by 5
• Every 6th number is divisible by 8
🚫 Common Mistakes to Avoid
Wrong Starting Point
Mistake: “It starts with 1, 1, 2, 3...”
Correct: It starts with 0, 1, 1, 2, 3...
Only Positive Numbers
Mistake: “Fibonacci numbers are always positive”
Correct: Can extend to negative numbers too!
Multiplication Instead
Mistake: “Each number is multiplied by the previous”
Correct: Each number is ADDED to the previous
Fibonacci Invented It
Mistake: “Fibonacci discovered this sequence”
Correct: He introduced it to Europe, but India knew it first!
🧠 Easy Ways to Remember It
🎯 The “Addition Game”
Step 1: Write down 0 and 1
Step 2: Add them: 0 + 1 = 1
Step 3: Add the last two: 1 + 1 = 2
Step 4: Keep going: 1 + 2 = 3
✋ The “Hand Method”
Left thumb: 0 (start here)
Left index: 1 (second number)
Left middle: 1 (0+1)
Keep adding: Use your fingers to track!
🎪 Fun Memory Tricks
Make a Song
“Zero-one-one-two-three-five-eight...” Sing it to your favorite tune!
Phone Number
Remember it like a phone number: 0-1-1-2-3-5-8-1-3
Draw Spirals
Draw the famous Fibonacci spiral - it helps visualize the pattern!
🌍 Where You'll Find Fibonacci in Real Life
The Fibonacci sequence isn't just math on paper - it's everywhere around us! Here are some amazing places you can spot it:
In Nature
- • Sunflower seed spirals (21, 34, 55, 89)
- • Pinecone and pineapple patterns
- • Flower petals (lilies have 3, buttercups have 5)
- • Tree branch arrangements
- • Nautilus shell chambers
In Art & Design
- • Mona Lisa's face proportions
- • Parthenon architecture
- • Modern logo designs (Apple, Twitter)
- • Photography composition
- • Music and rhythm patterns
In Technology
- • Computer algorithms
- • Data compression
- • Stock market analysis
- • Search engine optimization
- • Video game level design
In Architecture
- • Building proportions
- • Spiral staircases
- • Window arrangements
- • Garden layouts
- • Bridge designs
In Finance
- • Stock market predictions
- • Trading strategies
- • Economic modeling
- • Risk assessment
- • Investment patterns
In Science
- • DNA structure patterns
- • Galaxy spiral formations
- • Crystal growth patterns
- • Population dynamics
- • Weather pattern analysis
🎯 Try This at Home!
🌻 Count Sunflower Seeds
Next time you see a sunflower, count the spiral patterns in the center. You'll likely find 21, 34, 55, or even 89 spirals!
🌸 Check Your Garden
Count the petals on different flowers. Many will have 3, 5, 8, 13, or 21 petals - all Fibonacci numbers!
🎉 What We've Learned
The Big Picture
🔢 The Simple Rule
Start with 0 and 1, then each new number is just the sum of the two before it. That's it! From this simple rule comes incredible complexity and beauty.
🌍 Everywhere Around Us
From sunflower seeds to stock markets, from art masterpieces to computer algorithms - Fibonacci numbers appear in the most unexpected places!
The sequence that connects math to the universe!
📝 Quick Recap
The Rule
Add the previous two numbers
The History
Fibonacci brought it to Europe in 1202
The Magic
Connects to the golden ratio
The Nature
Found everywhere in the natural world
🚀 Ready to Explore More?
You've just scratched the surface! The Fibonacci sequence has so many more secrets waiting to be discovered.
🧮 Learn the Math
Discover the formulas and mathematical properties
🌿 Explore Nature
See amazing examples in plants, animals, and more