Have you ever wondered why sunflowers look so perfectly arranged? Or why pinecones seem to follow a specific pattern? The answer lies in one of mathematics' most fascinating sequences: the Fibonacci sequence. This magical mathematical pattern appears throughout nature in ways that will amaze and inspire you.
๐ฟ Quick Fibonacci Reminder
The Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
Each number is the sum of the two preceding ones. This simple rule creates patterns that nature has been using for millions of years!
๐ค Why Does Nature Use Fibonacci Patterns?
๐ฏ Efficiency
Fibonacci patterns allow plants to pack the maximum number of seeds, leaves, or petals into the smallest space while ensuring optimal sunlight exposure.
โ๏ธ Balance
The golden ratio (ฯ โ 1.618) that emerges from Fibonacci numbers creates the most aesthetically pleasing and structurally stable arrangements.
๐ก Nature's Optimization
Through millions of years of evolution, nature has โdiscoveredโ that Fibonacci patterns provide the most efficient solutions for growth, reproduction, and survival.
๐ 10 Amazing Examples of Fibonacci in Nature
๐ป 1. Sunflower Seed Spirals
The most famous example! Sunflower seeds arrange themselves in two sets of spirals: one clockwise and one counterclockwise. These spirals almost always follow consecutive Fibonacci numbers.
Common Patterns:
- โข Small sunflowers: 21 and 34 spirals
- โข Medium sunflowers: 34 and 55 spirals
- โข Large sunflowers: 55 and 89 spirals
- โข Giant sunflowers: 89 and 144 spirals
Sunflower with 34 and 55 spirals
Pinecone with 8 and 13 spirals
๐ฒ 2. Pinecone Scale Patterns
Pinecones display beautiful Fibonacci spirals in their scale arrangements. The scales are organized in two sets of spirals that wind around the cone in opposite directions.
Typical Patterns:
- โข Small pinecones: 5 and 8 spirals
- โข Medium pinecones: 8 and 13 spirals
- โข Large pinecones: 13 and 21 spirals
๐ 3. Nautilus Shell Chambers
The nautilus shell grows in a perfect logarithmic spiral that closely approximates the golden spiral derived from Fibonacci rectangles. Each chamber is larger than the previous one by a factor of the golden ratio.
Amazing Facts:
- โข Each chamber is ฯ (1.618) times larger
- โข The spiral maintains perfect proportions
- โข This design provides optimal strength
Nautilus shell golden spiral
๐ธ 4. Flower Petal Arrangements
Many flowers have petal counts that correspond to Fibonacci numbers. This isn't coincidenceโit's nature's way of optimizing petal arrangement for pollination.
Common Examples:
- โข Lilies: 3 petals
- โข Buttercups: 5 petals
- โข Delphiniums: 8 petals
- โข Marigolds: 13 petals
Why This Pattern?
- โข Optimal pollinator access
- โข Efficient petal packing
- โข Structural stability
- โข Aesthetic appeal
Flowers with Fibonacci petal counts
Tree branching following Fibonacci pattern
๐ณ 5. Tree Branch Patterns
Trees often follow Fibonacci patterns in their branching. Starting from the trunk, branches split following the sequence, creating optimal light exposure and structural support.
Branching Pattern:
- โข Level 1: 1 trunk
- โข Level 2: 1 main branch
- โข Level 3: 2 branches
- โข Level 4: 3 branches
- โข Level 5: 5 branches
- โข Level 6: 8 branches
๐ 6. Pineapple Diamond Patterns
Pineapples display stunning Fibonacci spirals in their diamond-shaped scale patterns. The spirals go in three directions, all following Fibonacci numbers.
Spiral Counts:
- โข Gentle left spirals: 8
- โข Steep left spirals: 13
- โข Right spirals: 21
All consecutive Fibonacci numbers!
Pineapple with 8, 13, and 21 spirals
More Amazing Examples
๐ฅฆ 7. Romanesco Broccoli
This stunning vegetable displays perfect Fibonacci spirals in a fractal pattern. Each floret is a smaller version of the whole!
Spiral counts: 5, 8, 13, 21
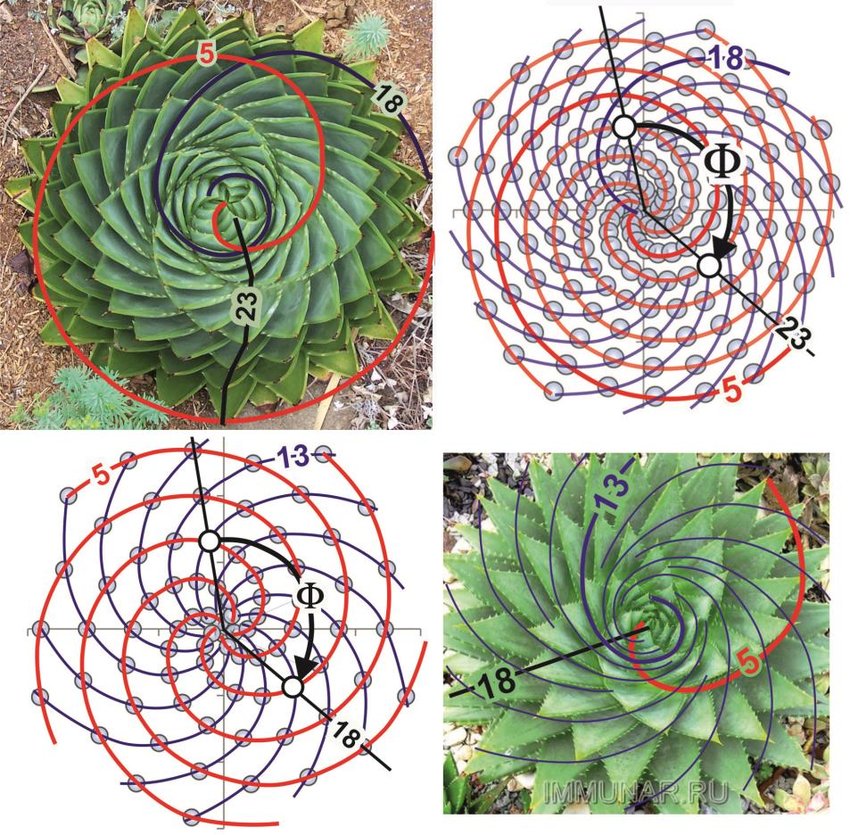
๐ต 8. Succulent Spirals
Aloe vera, echeveria, and other succulents arrange their leaves in perfect Fibonacci spirals for optimal water collection and sun exposure.
Common: 8, 13, 21 spirals
๐ผ 9. Seed Head Patterns
Dandelions, daisies, and other composite flowers arrange their seeds in Fibonacci spirals for optimal dispersal and packing efficiency.
Typical: 13, 21, 34 spirals
๐ 10. Leaf Phyllotaxis
Plants arrange their leaves around stems following Fibonacci angles (137.5ยฐ) to maximize sunlight exposure without shadowing lower leaves.
Golden angle: 137.5ยฐ
โจ The Golden Ratio Connection
As Fibonacci numbers get larger, the ratio between consecutive numbers approaches the golden ratio (ฯ โ 1.618). This magical number appears throughout nature and is considered the most aesthetically pleasing proportion.
Golden Ratio Examples:
- โข 8/5 = 1.6
- โข 13/8 = 1.625
- โข 21/13 = 1.615...
- โข 34/21 = 1.619...
- โข 55/34 = 1.617...
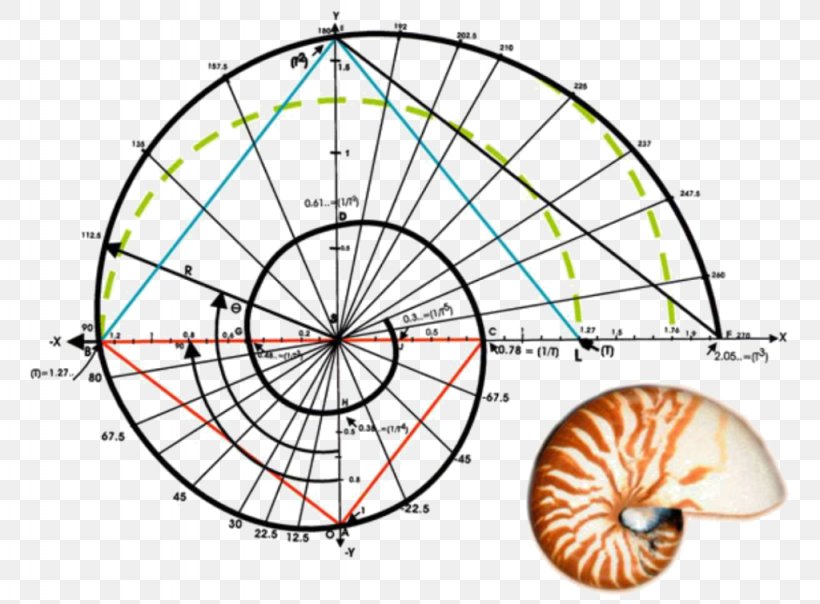
Golden spiral from Fibonacci rectangles
๐จ Why ฯ (Phi) is Special
Architecture
Parthenon, pyramids
Art
Da Vinci, Mondrian
Biology
DNA, human body
๐ How to Spot Fibonacci Patterns in Nature
What to Look For:
Spiral Patterns
Look for curved arrangements that wind outward
Count the Spirals
Count clockwise and counterclockwise spirals separately
Check the Numbers
See if they match Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21...
Best Places to Explore:
- ๐ปSunflower fields (summer)
- ๐ฒPine forests (pinecones)
- ๐ธBotanical gardens (various flowers)
- ๐๏ธBeaches (shells and sea life)
- ๐ฅฆFarmers markets (vegetables)
- ๐ฟYour own garden!
๐ฏ Fun Fibonacci Activities
Photo Hunt
Take photos of Fibonacci patterns you find in nature. Create your own collection!
Spiral Counter
Practice counting spirals on sunflowers, pinecones, and pineapples.
Draw Spirals
Try drawing your own Fibonacci spirals using the golden rectangle method.
๐ The Magic Continues
The Fibonacci sequence in nature reveals the profound connection between mathematics and the natural world. From the tiniest flower petals to the grandest spiral galaxies, this simple sequence governs patterns that have evolved over millions of years.
Next time you're outdoors, take a moment to look for these patterns. You'll be amazed at how often you spot them once you know what to look for. Nature truly is the greatest mathematician of all!
๐ Ready to Explore More?
Dive deeper into the mathematical world of Fibonacci sequences and discover the formulas behind these natural patterns.
Related Articles
What is Fibonacci Sequence?
Learn the basics of this fascinating mathematical pattern
8 min read โFibonacci Sequence Formula
Discover the mathematical formulas behind the sequence
15 min read โComing Soon
Fibonacci Examples in Math & Art
Explore applications across various fields